目录
- )
- 括号匹配判断
题目、有效的括号字符串(1):【两个栈】
给定一个只包含三种字符的字符串:( ,) 和 *,写一个函数来检验这个字符串是否为有效字符串。有效字符串具有如下规则:
- 任何左括号
(必须有相应的右括号)。 - 任何右括号
)必须有相应的左括号(。 - 左括号
(必须在对应的右括号之前)。 *可以被视为单个右括号),或单个左括号(,或一个空字符串。- 一个空字符串也被视为有效字符串。
示例 1:
输入: "()"输出: True
示例 2:
输入: "(*)"输出: True
示例 3:
输入: "(*))"输出: True
思路1:时间O(n2),空间O(n)
采用1个栈存(),同时存索引
采用第2个栈存*,同时存索引
两个for循环比较两个栈。
代码:
def checkValidString(self, s): """ :type s: str :rtype: bool """ #采用两个栈来解决 if not s: return True n = [] stack = [] for i,ss in enumerate(s): if ss == '(': stack.append((i,ss)) elif ss == ')': if stack and stack[-1][1] == '(': stack.pop() else: stack.append((i,ss)) elif ss == '*': n.append(i) print(stack) i , j = 0 , 0 ca = True while i < len(stack): while j < len(n) and len(stack) > 0: if stack[i][1] == ')' and stack[i][0] >= n[j] or (stack[i][1] == '(' and stack[i][0] <= n[j]): stack.pop(i) n.pop(j) ca = False j -= 1 j += 1 if ca: i += 1 if j == len(n): break if len(stack) != 0: return False return True 思路2:时间O(n),空间O(1)
left变量: * 作为( 时,左括号(的数量
right变量:*作为 )时,左括号(的数量
如果left<0,返回False
如果循环结束,right > 0,就返回False
def checkValidString(s): if not s: return True left , right = 0,0 for ss in s: left += 1 if ss != ')' else -1 right += 1 if ss == '(' else -1 if left < 0: return False right = max(right ,0 ) return right == 0 题目、括号的有效性(2)

思路:采用两个变量记录‘(’,‘)’数量
- 遍历,判断每个字符是否为'('')',否则不合法。
- 遍历同时,采用left和right记录'(',‘)’的数量,若到目前为止,‘)’比‘(’多,则不合法
- 遍历后,如果‘(’和‘)’数量不等,则不合法
代码:
def isValid(s): if not s or s == '': return False status = 0 #记录')'减去‘(’的数量 for ss in s: if ss != '(' and ss != ')': return False if ss == '(': status += 1 elif ss == ')': status -= 1 if status < 0: return False return status == 0s = '((()()))'isValid(s) 原问题思路:采用一个变量记录‘)’减去‘(’的差,若当前)-(>0则返回FALSE
题目、判断括号字符串是否有效(3)
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
示例 1:
输入: "()"输出: true
示例 2:
输入: "()[]{}"输出: true 思路:采用栈,遇到左括号入栈,右括号出栈。出栈与当前符号不匹配,则不有效。
代码:
def isValid(self, s): """ :type s: str :rtype: bool """ if not s: return True stack = [] for ss in s: if ss == '(' or ss == '{' or ss == '[': stack.append(ss) elif ss == ']': if stack and stack[-1] == '[': stack.pop() else: return False elif ss == ')': if stack and stack[-1] == '(': stack.pop() else: return False elif ss == '}': if stack and stack[-1] == '{': stack.pop() else: return False return len(stack) == 0
题目、最长有效括号子串
给定一个括号字符串,求最长的有效括号子串。

思路:动态规划,时间O(N),空间O(N)
dp[i]表示从0到第i个字符串的最长有效括号子串。
需同时考虑两种情况:
- 包含关系(()),dp[i] = dp[i-1] + 2【若 s [ i ] == ')' ,且 s [ i - dp [i-1] -1 ] == '('】
- 并列关系()(),dp[i] = dp[i] + dp [ i - dp [i-1] -2 ]
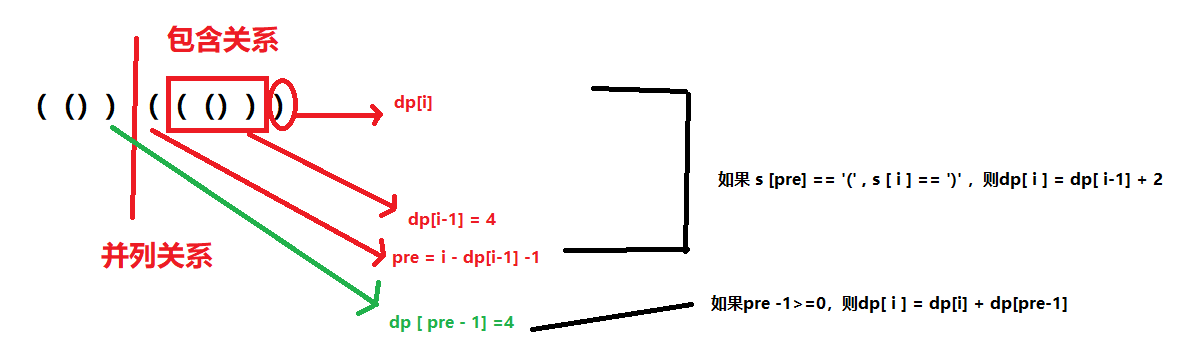
if not s or len(s) <= 1: return 0 dp = [0] * len(s) res = 0 for i in range(1,len(s)): if s[i] == ')': pre = i - dp[i-1] -1 if pre >= 0 and s[pre] == '(': #若(())这种包含关系,需加dp[i-1]+2. dp[i] = dp[i-1] + 2 #若()()这种并列关系,需加上dp[pre-1] if pre > 0: dp[i] += dp[pre-1] res = max(res,dp[i]) return res
题目:856括号的分数【栈】
给定一个平衡括号字符串 S,按下述规则计算该字符串的分数:
()得 1 分。AB得A + B分,其中 A 和 B 是平衡括号字符串。(A)得2 * A分,其中 A 是平衡括号字符串。
示例 1:
输入: "()"输出: 1
示例 2:
输入: "(())"输出: 2
示例 3:
输入: "()()"输出: 2
示例 4:
输入: "(()(()))"输出: 6
提示:
S是平衡括号字符串,且只含有(和)。2 <= S.length <= 50
思路:
初始 index = 0 ,初始结果列表 stack= [0]*30 【30是一个随意值,防止超出界限,stack用来存结果的。】
①遇到’(‘,index往前一步,遇到’)‘,index往后退一步
②遇到’(‘,stack[index] += max(stack[index+1],1),遇到’)‘,stack[index] = 0
代码:
def scoreOfParentheses(self, S): res, i = [0] * 30, 0 for c in S: i += 1 if c == '(' else -1 res[i] = res[i] + max(res[i + 1] * 2, 1) if c == ')' else 0 return res[0]
题目:22括号生成【递归】卡诺兰数
给出 n 代表生成括号的对数,请你写出一个函数,使其能够生成所有可能的并且有效的括号组合。
例如,给出 n =3,生成结果为:
[ "((()))", "(()())", "(())()", "()(())", "()()()"]
思路:
递归条件1:left>0,则递归helper(string+'(',res,left - 1 ,right)
递归条件2:left<right,则递归helper(string+')',res,left,right-1)
代码:
class Solution(object): def generateParenthesis(self, n): """ :type n: int :rtype: List[str] """ if n == 0: return [] res = [] def helper(subStr,res,left,right): if left == 0 and right == 0: res.append(subStr) return if left > 0: helper(subStr+'(',res,left-1,right) if left
题目:字符串解码
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例:
s = "3[a]2[bc]", 返回 "aaabcbc".s = "3[a2[c]]", 返回 "accaccacc".s = "2[abc]3[cd]ef", 返回 "abcabccdcdcdef".
思路:
采用一个栈存储字母和数字num,【【字母1,数字1】,【字母2,数字2】……】
遇到字母就加入栈的最后一个元素的字母中,
遇到数字,num 存储该数字
遇到 '[' ,栈就新增一个元素,元素包含前面数字num
遇到 ']' , 栈就弹出最后一个元素,字母*元素,再加入前一个元素的字母中
代码:
class Solution(object): def decodeString(self, s): """ :type s: str :rtype: str """ if not s: return s res = [["",1]] num = '' for ss in s: if ss.isdigit(): num += ss elif ss == '[': res.append(["",int(num)]) num = '' elif ss.isalpha(): res[-1][0] += ss elif ss == ']': k,v = res.pop() res[-1][0] += k*v return res[0][0]
题目:交错字符串

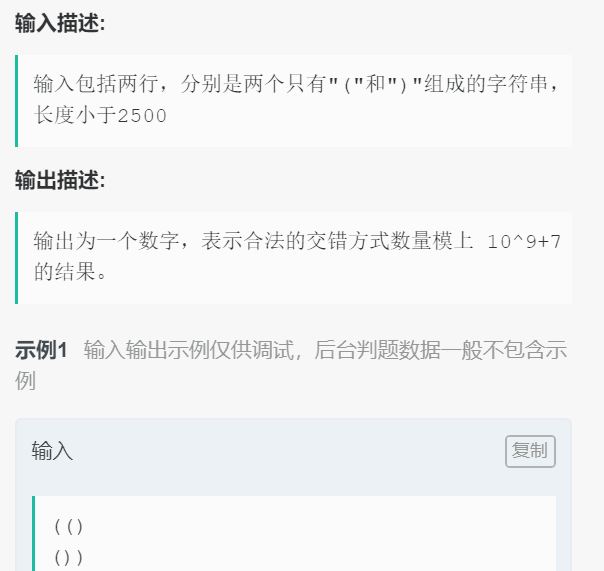
结果为19。
分析:

